Abstract : This paper studies a method of data processing using FPGA, which includes extracting the data of high log 2M bits of input data, and as the high effective bit, searching for the high effective bit according to the calculation table of the preset objective function. Corresponding objective function value y(n) and objective function value y(n+1) corresponding to high significant bit +1; extracting remaining bit data of the input data as the low significant bit, and the low effective bit and y Multiplying the difference between (n) and y(n+1) to obtain an offset value off(n), which is added to the objective function value y(n) corresponding to the high significant bit, and will be calculated The result is the objective function value corresponding to the input data. The method has the characteristics of simple control, structural rules, single operation period and high calculation precision, and is suitable for data processing implementation of FPGA. Introduction Field Programmable Gate Array (FPGA) chips are widely used in many fields, especially in the field of wireless communications. FPGAs are extremely real-time and parallel processing, making it possible to process signals in real time. The FPGA usually contains logic cells (lookup tables/flip-flops), memory cells (BRAMs), multiply-accumulate cells (MACs), and some other clocks, pin units, etc. [1-3]. The main development trend of modern digital signal processing is: the structure of the algorithm is increasingly complex, the calculation is large, the real-time requirements are high, and a large number of complex functions such as trigonometric functions, square roots, and logarithms are calculated. However, the internal multiplication and addition unit of FPGA is not suitable for the calculation of such functions directly. It is necessary to decompose various complex functions into simple shift, addition and multiplication structures, and then implement them in FPGA [4]. Currently, the calculation of complex functions such as trigonometric functions, square roots, and logarithms on FPGAs is the most common in the technical field, followed by square roots and trigonometric functions, and rarely involves logarithms and other complex functions. In the specific implementation of FPGA, such functions generally use the direct table lookup method or the power series expansion method. For the trigonometric function and the square root calculation, the CORDIC calculation method is also used, but the application of these three methods has Certain limitations [4]. 1 Existing FPGA implementation method (1) Using the direct table lookup method on the FPGA to implement the function calculation, has: Table 1 Memory cells required for different input and output bit widths It can be seen that when the input and output bit width is small, the direct look-up table method can meet the implementation requirements, but in the field of digital signal processing, the input and output are generally above 16 bits, and it is difficult to meet the implementation requirements by using the direct look-up table method. Here is an example of a square root algorithm. There are two ways to perform the square root calculation using the direct look-up table method. Method 1: Under the condition of fully guaranteeing accuracy, the direct look-up table method is adopted. If the input is 16bits input 16bits output, under the condition of fully guaranteed accuracy, the FPGA needs to store 216 depth data, requiring 64 18k BRAM storage space. A medium-sized FPGA generally contains tens to hundreds of 18k BRAM memory cells. At this time, most of the memory cells are used in the calculation, which obviously does not meet the resource requirements of the implementation. Method 2: Reduce the accuracy, reduce the input bit width, and adopt the direct look-up table method. Table 2 Direct look-up table method It can be seen that as the actual effective input increases, the calculation accuracy becomes larger, and it is difficult to satisfy the calculation error requirement. (2) Calculate the function using the power series expansion method on the FPGA. If the input is 16 bits, the block diagram of the power series expansion method is shown in Figure 1. Figure 1 Power series expansion method to achieve exp calculation In addition, the application range of power series expansion method is also limited. The calculation of square root, reciprocal, logarithm and trigonometric function can be performed by power series expansion method. However, for more complicated function calculation, it is no longer suitable for calculation with this method. . (3) The CORDIC method is used on the FPGA to implement the function calculation. 2 The method proposed in this paper uses two-level method for function calculation on FPGA: the first stage directly uses the high-effective bits of the input data to determine the effective range of the calculation result; the second level directly uses the low-effective bits of the input data to calculate The error adjustment of the result. The research method makes full use of various logic resources, multipliers (or multipliers) resources and BRAM resources inside the FPGA: the corresponding depth data table can be used to store the effective range of the first level data according to the size of the internal BRAM resources of the FPGA; The multiply-accumulator (or multiplier) resource inside the FPGA performs a multiply-accumulate operation. The method has the characteristics of simple control, structural rules, single operation cycle and high calculation precision, and is suitable for FPGA algorithm implementation. In addition, using the two-level calculation method of this research method, the calculation methods of different functions are consistent. As long as the data in the first-level calculation of the high-effective data table is modified, the design can be reused, which is beneficial to resource sharing and modular implementation. . Figure 2 FPGA two-stage method for function calculation Comparative analysis with existing programs: Table 3 Comparison of the two-level calculation method and the direct table look-up method error table (2) Comparison with power series expansion method First, the new method of this problem is more widely used than the power series expansion method. Secondly, under the same function, taking the calculation of exp as an example, the new method proposed in this paper has better resources and less error. In terms of resources, the two-level calculation method used on the FPGA can only calculate two multipliers at the same time, which is far less than the resource consumption of the power series expansion method; in terms of error, in the range of 0 to π/4, 16 bits The maximum error of input, cosΦ and sinΦ is less than 10-5, so the error of this method is smaller than that of power series expansion. (3) Comparison with CORDIC method Firstly, the new method proposed in this paper is more widely used than the power series expansion method. Secondly, under the same function, taking the calculation of exp as an example, the new method consumes relatively little resources. CosΦ and sinΦ only need about 300 LUT/FFs at the same time. Moreover, the new method uses a single-period cycle mode with a higher computational speed. Our
company offers rubber, and specialty seal and o-ring for molding electronic and electrical Connectors, both circular
and rectangular types. We have in house capabilities and quick turn
around.
Cable Grommets with various Grommet Shapes, Rib Styles, Slot Shapes, Inner Flanges,
and Colors - To have access to our 3D Cable Grommet Design Tool
Silicone Rubber Products,Cable Silicone O-Ring,Rubber Seal,Custom Silicone Seal,Waterproofing O-Ring,Tpe Grommet ETOP WIREHARNESS LIMITED , https://www.oemwireharness.com
Advantages - strong versatility and simple structure;
Disadvantages - As the input bit width increases, the consumption of internal storage increases exponentially.
Table 1 shows the memory cells (BRAM) required for different input and output bit widths. 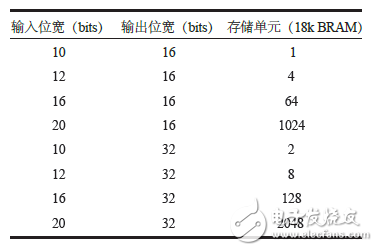
Advantages - the calculation accuracy is controllable, and multi-level expansion can achieve higher calculation accuracy;
Disadvantages - Power series expansion method In order to achieve higher precision, multi-level expansion is required, which requires more resources to be implemented.
Taking exp as an example (within the range of 0 to π/4), a trigonometric power series expansion method is used: 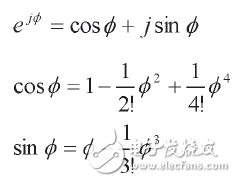
From the perspective of resources, the implementation of the trigonometric power series expansion method in FPGA requires 5 levels of multiplication and 3 stages of addition. Considering the multiplication of each stage, the bit width needs to be expanded. Actually, 12 multipliers (18 bits & TImes; 18 bits) of the FPGA are needed. In addition, from the aspect of error, the maximum error of cosΦ is 0.046% in the range of 0 to π/4, and the maximum error of sinΦ is 0.35%. 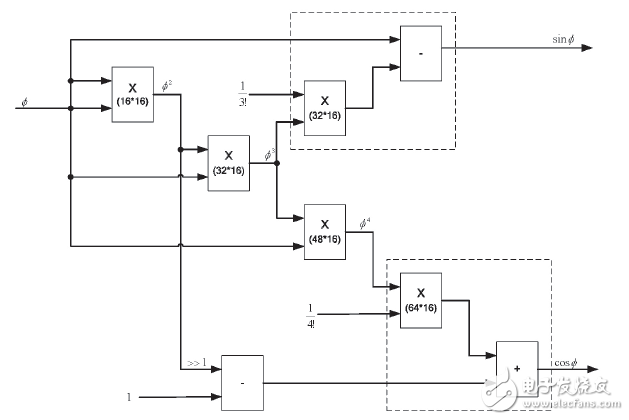
Advantages: Decompose complex operations into simple shifts, plus iterative operations, structural rules, and computational cycles can be predicted, which is more suitable for FPGA implementation;
Disadvantages: Generally, the multi-cycle mode is adopted, and the resource consumption in the single-cycle mode is high, and the calculation is limited to a limited range such as vector rotation and square root.
Using CORCIC to calculate the trigonometric function, 16bits input requires 500 LUT/FFs under multi-cycle conditions, and 1000 cycles of LUT/FFs are required under single-cycle conditions. 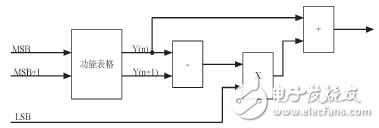
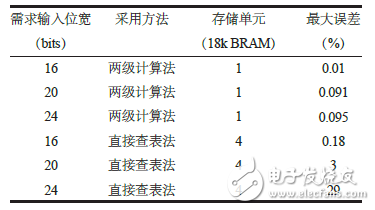
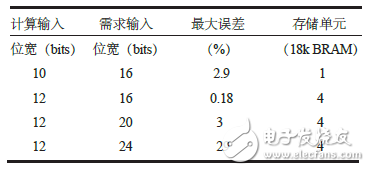
(1) Comparison with the direct look-up table method Taking the prescribing party as an example, the list of resources and errors is shown in Table 3. It can be seen that in terms of resources and errors, the research method has obvious advantages in implementing function calculation on FPGA. In addition, FPGAs can further increase computational accuracy by adding memory cells and extending the output bit width.