Detailed analysis of Fourier transform, Laplace transform, z transform

1. About the Fourier transform transform? A: The fourier transform transforms the continuous time domain signal into the frequency domain; it can be said to be a special case of the laplace transform, which is a generalization of the fourier transform. The existence condition is wider than the fourier transform, and the continuous time domain signal is transformed to The complex frequency domain (the entire complex plane, and the fourier transform can be seen as only the jΩ axis at this time); the z transform is the laplace transform of the discrete signal after the continuous sampling of the continuous signal, and then the transformation result when z=e^sT (T is the sampling period), the corresponding domain is the digital complex frequency domain, in which case the digital frequency ω = ΩT. - Refer to Zheng Junli's "Signals and Systems."

The essence of the Fourier transform is to separate a signal into an additive of an infinite number of sinusoidal/complex exponential signals, that is, to convert the signal into a form of sinusoidal signal addition - since there are infinitely many signals added, then For non-periodic signals, the weight of each signal should be zero—but there is a difference in density. You can think about the probability density in probability theory—the probability of falling to each point is infinitely small. But these infinitesimals are different. Therefore, after the Fourier transform, the abscissa is the frequency of the separated sinusoidal signal, and the ordinate corresponds to the weighted density. For periodic signals, since the sine wave components of certain frequencies can indeed be extracted, the weighting is not zero - in the magnitude spectrum, it is infinitely large - but these infinities are obviously different, so we Expressed by the impulse function. It has been said that the Fourier transform is to represent various forms of signals with sinusoidal signals, so that a non-sinusoidal signal is Fourier transformed, and a component different from the original signal frequency is obtained - all of which are integer multiples of the original signal frequency. These high frequency signals are used to modify the sinusoidal signal with the same frequency as the original signal, bringing it closer to the original signal. Therefore, the lowest frequency peak in the spectrum (often the highest in amplitude) is the original signal frequency. The Fourier transform transforms the signal from the time domain to the frequency domain. Therefore, it is meaningless to splicing the signals of different frequencies in the time domain to perform Fourier transform. In actual cases, we collect signals every time to transform. In order to reflect the change of the signal over time in the frequency domain. My language may be awkward, but I have done my best to tell you about my understanding - I really hope that it will be useful to you. I haven't answered the question for a long time. The reason why I answered this question is because I really benefited from the process of learning the Fourier transform and the Laplace transform. They almost changed my world. Awareness. The Fourier transform is worthy of your understanding - even if it is worthwhile to think about it for a few months - I thought about it as long as it would be a problem. However, Zheda’s school motto “seeking truth” has always spurred me to pursue an understanding of the theory – and finally realized through a very painful speculation. I suggest you take a look at our Signals and Systems course materials: Chemical Industry Press's Signals and Systems, which will help. (Another statement) For the periodic function f, the Fourier transform is to decompose this function into the sum of a number of sinusoidal functions fn, each fn having a frequency n times f. The so-called second harmonic is the function whose function f2 is twice the frequency of f. (The other two statements) The meaning of the Fourier series of the periodic signal is the amplitude of the signal at each discrete frequency component; the Fourier transform of the aperiodic signal can be understood as the Fourier series of the periodic signal with periodic infinity . At this time, the discrete frequency gradually becomes a continuous frequency, and the spectral density value at a certain frequency is meaningless. Like the probability density function, you only have to find the area value formed by the spectral density function in a small frequency near that point. It only makes sense to indicate the amplitude of the signal at that frequency point. For specific reference to "Signal and System" Zheng Junli version of Tsinghua University Press P91, P111.
2. What is a Laplace transform? answer:

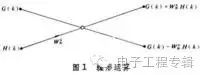
(1st statement) The role of the Laplace transform:

(1) Solving the equation is simplified. And the initial conditions are automatically included in the transformation.

(2) The Laplace transform transforms "differential" into "multiplication" and "integration" into "division". The differential equation is transformed into an algebraic equation. The Laplace transform transforms the convolution operation in the time domain into a "multiplication" operation.

(3) Using the system function zero point, pole distribution analysis system rules.

In the classical control theory, the analysis and synthesis of the control system are based on the Laplace transform. One of the main advantages of introducing a Laplace transform is that a transfer function can be used instead of a differential equation to describe the characteristics of the system. This is an intuitive and simple graphical method to determine the overall characteristics of the control system (see signal flow diagram, dynamic structure diagram), analysis of the motion process of the control system (see Nyquist stability criterion, root locus method), and The correction device of the integrated control system (see Control System Calibration Method) offers the possibility.

Now give you an example: When we learn to control, such as a second-order circuit RLC system differential equation is: LC * Uc ' ' + RC * Uc ' + Uc = U imagine you borrow this differential equation more difficult, then you use Laplace transform, the differential equation becomes LC*s^2*Uc+RCs*Uc+Uc=U then Uc=U/(LCs^2+RCs+1) and then the result can be directly obtained by looking up the table (just check the score table) Just as convenient), this is no better than solving differential equations.

(Phase 2) Laplace transform provides a transform domain method that maps signals (functions) defined in the time domain to complex frequency domains. To understand this sentence, you need to understand the function space. The concept - we know that a function defines a relationship from "a set of elements to an element of another set", and a set of two or more functions is a function space, that is, a function space is also a set The "definite domain" of the Laplace transform is the function space. It can be said that the Laplace transform is a function of the processing function. Since the Laplace transform is quite cleverly defined, it has some strange features. Trait), and this is a one-to-one correspondence (as long as the convergence domain of the complex frequency domain is given), so as long as a time domain function (signal) is given, it can be transformed into a Laplacian transform. Complex frequency domain signal (whether this signal is a real signal or a complex signal), so as long as we process this complex frequency domain signal, it is equivalent to processing the time domain signal (for example, f (t) ←→F(s), Re[s]>a, then if we delay the processing of F(s) and get the signal F(sz), Re[s]>a+Re[z], then It is equivalent to multiplying the time domain function by a rotation factor e^zt, ie f(t)e^zt←→F(sz), Re[s]>a+Re[z]; as long as F(sz) By performing an inverse transformation, we can get f(t)e^zt).

The Laplace transform is used to solve differential equations, mainly by applying several properties of the Laplace transform, which transforms the differential equations into solving algebraic equations (because solving algebraic equations is always much easier than solving differential equations! Moreover, (It is convenient to perform a Laplace inverse transformation on the solution result to obtain the solution of the original differential equation).

We can always draw an image of the real function (which is true for most functions), but it is difficult to draw an image of a complex function, which may be one of the reasons for the abstraction of the Laplace transform; Another reason is that the complex frequency s in the Laplace transform has no clear physical meaning. Regarding the feature root and the plural, it is recommended that the questioner should look at the definition in the book again. It should be easy to understand.
3. What is z transformation?

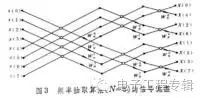
The mathematical transformation of a sequence of functions established in a discrete system analysis to simplify the operation is similar to the Laplace transform in the analysis of continuous systems. Z transform is a simple and effective method for solving linear difference equations. In the theory of sampling control, Z transform is the main mathematical tool. Z-transformation is also widely used in time series analysis, data smoothing, digital filtering and other fields. When a continuous signal x(t) passes through a sampling switch that is closed every T seconds, a function sequence x(kT) (k = 0, 1, 2, ...) is obtained. The function sequence x(kT) has the same function value as the continuous signal x(t) at times 0, T, 2T, ..., and is always zero at all other times. 4. What is FFT (fast fourier transform)? A: Audio processing is commonly used inside. It is to transform the waveform (time domain signal) into the frequency domain, so that the user can better analyze. The frequency domain is a spectrum similar to “Thousands of Listeners”. This process is called Discrete Fourier Transform (DFT). The FFT is an efficient and fast algorithm for DFT. The principle of the fast Fourier transform algorithm is (from Baidu Encyclopedia): Fast Fourier Transform (FFT) is a fast algorithm of discrete Fourier transform, which is based on the odd, even, imaginary, and real properties of discrete Fourier transforms. The transformed algorithm is improved. It has no new findings on the theory of Fourier transform, but it can be said that it is a big step for applying discrete Fourier transform in computer systems or digital systems. Let x(n) be a complex sequence of N terms, which is transformed by DFT. Any X(m) calculation requires N complex multiplications and N-1 complex additions, while one complex multiplication is equal to four real multiplications and two times. Real addition,

A complex addition is equal to two real additions. Even if one complex multiplication and one complex addition are defined as one "operation" (four real multiplications and four real additions), then X(m) of the N-order complex sequence is obtained, that is, The N-point DFT transform requires approximately N2 operations. When N=1024 points or more, N2=1048576 operations are required. In the FFT, an N-term sequence (N=2k, k is a positive integer) is divided into two by using the periodicity and symmetry of WN. Two sub-sequences of N/2 terms, each N/2-point DFT transform requires (N/2) 2 operations, and then N times operations are used to combine two N/2-point DFT transforms into one N-point DFT Transform. After this transformation, the total number of operations becomes N+2(N/2)2=N+N2/2. Continuing with the above example, when N=1024, the total number of operations becomes 525,312 times, saving about 50% of the computation. And if we continue this "divided into two" ideas until the DFT operation unit is divided into two groups, then the N-point DFT transformation requires only Nlog2N operations, and N is at 1024 points. The amount is only 10240 times, which is 1% of the previous direct algorithm. The more points, the greater the computational savings, which is the superiority of FFT.